L’américain Mathworks, l’éditeur de logiciels pour les calculs mathématiques (Matlab et Simulink), vient d’ajouter à Matlab la boîte à outils 5G. Elle fournit les formes d’onde conformes aux standards et des exemples de référence pour la modélisation, la simulation et la vérification de la couche physique des systèmes de communication 3GPP 5G New Radio (NR).
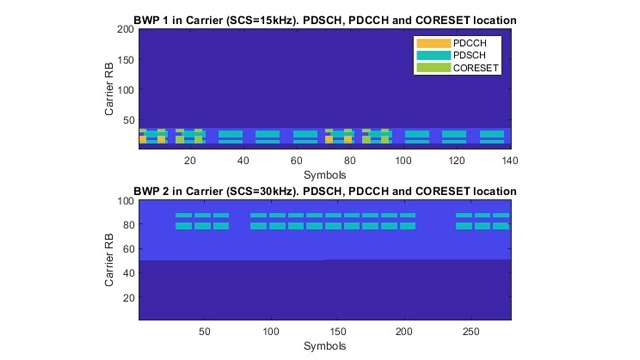
Les ingénieurs utilisant la 5G Toolbox peuvent rapidement concevoir des algorithmes critiques et prévoir les performances de liaison de bout-en-bout des systèmes conformes à la spécification 5G Version 15. Ils peuvent en effet générer des formes d'onde OFDM basées sur les espacements de sous-porteuse NR et les numérologies de trame, y compris les parties de largeur de bande de porteuse (CBP).
Parmi les autres fonctionnalités, on trouve les simulations au niveau des liaisons (analyse des performances de la liaison, test de débit, etc.), la simulation du traitement des liaisons descendantes 5G NR, la configuration et la génération des canaux de transport de liaison descendante (BCH, DL-SCH) et des informations de contrôle (codage LDPC, Polar Coding), ainsi que les simulations de taux d'erreur sur les blocs (BLER) avec des modèles de canal de propagation 5G NR TR 38.901, les procédures de recherche et de sélection de cellules pour obtenir les informations système initiales, y compris le bloc d'informations principal (MIB).
« Lorsqu'ils adoptent la 5G, les ingénieurs sans fil doivent vérifier que leur conception de produits peuvent être conformes ou coexister avec une nouvelle norme complexe qui continuera d'évoluer. Très peu d'entreprises disposent des ressources ou de l'expertise interne nécessaires pour comprendre et mettre en œuvre une conception conforme à la 5G », indique Ken Karnofsky, Senior Strategist Signal Processing Applications de MathWorks.